IMPLEMENTATION OF AVL TREES INSERTION, DELETION OPERATIONS
Exercise.No:8
TO LEARN C PROGRAMMING FOLLOW THIS YOUTUBE CHANNEL: Code with u - YouTube
AIM:
To write the program to implement AVL Tree and its operation.
ALGORITHM:
For Insertion:
Step 1: First, insert a new element into the tree using BST's (Binary Search Tree) insertion
logic.
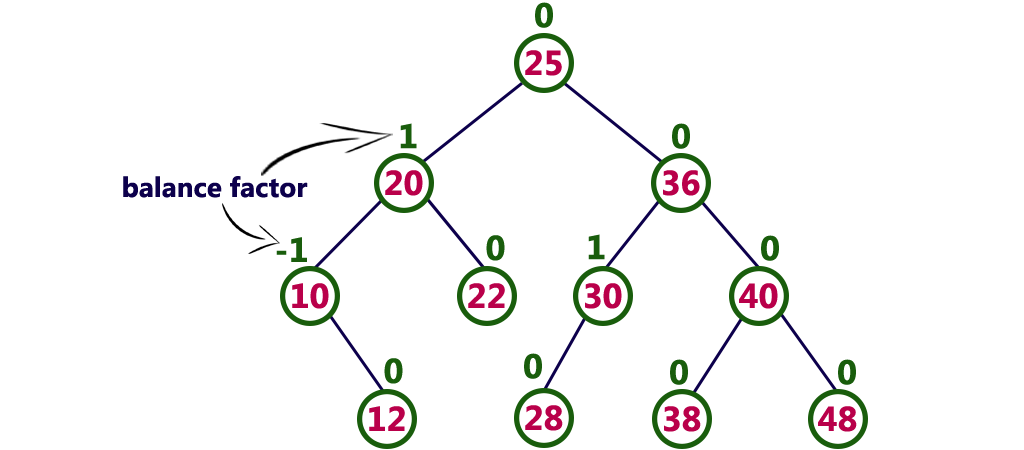
Step 2: After inserting the elements you have to check the Balance Factor of each node.
Step 3: When the Balance Factor of every node will be found like 0 or 1 or -1 then the
algorithm will proceed for the next operation.
Step 4: When the balance factor of any node comes other than the above three values then the
tree is said to be imbalanced. Then perform the suitable Rotation to make it balanced
and then the algorithm will proceed for the next operation.
For Deletion:
Step 1: Firstly, find that node where k is stored
Step 2: Secondly delete those contents of the node (Suppose the node is x)
Step 3: Claim: Deleting a node in an AVL tree can be reduced by deleting a leaf. There are
three possible cases:
• When x has no children then, delete x
• When x has one child, let x' becomes the child of x.
• Notice: x' cannot have a child, since sub trees of T can differ in height by at
most one then replaces the contents of x with the contents of x'
• then delete x' (a leaf)
• then find x's successor z (which has no left child)
• then replace x's contents with z's contents, and
• delete z
Step 4: When x has two children,
AVL Tree Rotations:
In AVL tree, after performing every operation like insertion and deletion we need to check
the balance factor of every node in the tree. If every node satisfies the balance factor
condition then we conclude the operation otherwise we must make it balanced. We use
rotation operations to make the tree balanced whenever the tree is becoming imbalanced due
to any operation.
Single Left Rotation (LL Rotation):
In LL Rotation every node moves one position to left from the current position.
Single Right Rotation (RR Rotation):
In RR Rotation every node moves one position to right from the current position.
Left Right Rotation (LR Rotation):
The LR Rotation is combination of single left rotation followed by single right rotation. In
LR Rotation, first every node moves one position to left then one position to right from the
current position.
Right Left Rotation (RL Rotation)
The RL Rotation is combination of single right rotation followed by single left rotation. In
RL Rotation, first every node moves one position to right then one position to left from the
current position.
Time Analysis of AVL Trees:
AVL tree is binary search tree with additional property that difference between height of left
sub-tree and right sub-tree of any node can’t be more than 1.
PROGRAM:
#include<conio.h>
#include<stdio.h>
#include<stdlib.h>
typedef struct node
{
int data;
struct node *left,*right;
int ht;
}node;
node *insert(node *, int);
node *Delete(node *, int);
void preorder(node *);
void inorder(node *);
int height( node *);
node *rotateright(node *);
node *rotateleft(node *);
node *RR(node *);
node *LL(node *);
node *LR(node *);
node *RL(node *);
int BF(node *);
void main()
{
node *root=NULL;
int x, n, i, op;
do
{
printf("\n1)Create ");
printf("\n2)Insert ");
printf("\n3)Delete ");
printf("\n4)Print ");
printf("\n5)Quit ");
printf("\n Enter Your Choice: ");
scanf("%d",&op);
switch(op)
{
case 1:printf("\n Enter no.of elements:");
scanf("%d",&n);
printf("\n Enter tree data:");
root=NULL;
for(i=0; i<n; i++)
{
scanf("%d",&x);
root=insert(root,x);
}
break;
case 2:printf("\n Enter a data : ");
scanf("%d",&x);
root=insert(root,x);
break;
case 3:printf("\n Enter a data : ");
scanf("%d",&x);
root=Delete(root,x);
break;
case 4: printf("\n Preorder sequence :\n");
preorder(root);
printf("\n Inorder sequence :\n");
inorder(root);
break;
}
}while(op<5);
}
node * insert(node *T, int x)
{
if(T==NULL)
{
T=(node*)malloc(sizeof(node));
T->data=x;
T->left=NULL;
T->right=NULL;
}
else
if(x > T->data)
{
T->right=insert(T->right,x);
if(BF(T)==-2)
if(x>T->right->data)
T=RR(T);
else
T=RL(T);
}
else
if(x<T->data)
{
T->left=insert(T->left,x);
if(BF(T)==2)
if(x < T->left->data)
T=LL(T);
else
T=LR(T);
}
T->ht=height(T);
return(T);
}
node * Delete(node *T, int x)
{ node *p;
if(T==NULL)
{
return NULL;
}
else
if(x > T->data)
{
T->right=Delete(T->right,x);
if(BF(T)==2)
if(BF(T->left)>=0)
T=LL(T);
else
T=LR(T);
}
else
if(x<T->data)
{
T->left=Delete(T->left,x);
if(BF(T)==-2)
if(BF(T->right)<=0)
T=RR(T);
else
T=RL(T);
}
else
{
if(T->right !=NULL)
{
p=T->right;
while(p->left != NULL)
p=p->left;
T->data=p->data;
T->right=Delete(T->right, p->data);
if(BF(T)==2)
if(BF(T->left)>=0)
T=LL(T);
else
T=LR(T);
}
else
return(T->left);
}
T->ht=height(T);
return(T);
}
int height(node *T)
{
int lh, rh;
if(T==NULL)
return(0);
if(T->left==NULL)
lh=0;
else
lh=1+T->left->ht;
if(T->right==NULL)
rh=0;
else
rh=1+T->right->ht;
if(lh>rh)
return(lh);
return(rh);
}
node * rotateright(node *x)
{
node *y;
y=x->left;
x->left=y->right;
y->right=x;
x->ht=height(x);
y->ht=height(y);
return(y);
}
node * rotateleft(node *x)
{
node *y;
y=x->right;
x->right=y->left;
y->left=x;
x->ht=height(x);
y->ht=height(y);
return(y);
}
node * RR(node *T)
{
T=rotateleft(T);
return(T);
}
node * LL(node *T)
{
T=rotateright(T);
return(T);
}
node * LR(node *T)
{
T->left=rotateleft(T->left);
T=rotateright(T);
return(T);
}
node * RL(node *T)
{
T->right=rotateright(T->right);
T=rotateleft(T);
return(T);
}
int BF(node *T)
{
int lh, rh;
if(T==NULL)
return(0);
if(T->left==NULL)
lh=0;
else
lh=1+T->left->ht;
if(T->right==NULL)
rh=0;
else
rh=1+T->right->ht;
return(lh-rh);
}
void preorder(node *T)
{
if(T!=NULL)
{
printf(" %d(Bf=%d)", T->data, BF(T));
preorder(T->left);
preorder(T->right);
}
}
void inorder(node *T)
{
if(T!=NULL)
{
inorder(T->left);
printf(" %d(Bf=%d)", T->data, BF(T));
inorder(T->right);
}
}
OUTPUT:
1)Create:
2)Insert:
3)Delete:
4)Print:
5)Quit:
Enter Your Choice: 1
Enter no.of elements :4
Enter tree data: 2
4
5
6
1)Create:
2)Insert:
3)Delete:
4)Print:
5)Quit:
Enter Your Choice: 4
Preorder sequence:
4(Bf=-1) 2(Bf=0) 5(Bf=-1) 6(Bf=0)
Inorder sequence:
2(Bf=0) 4(Bf=-1) 5(Bf=-1) 6(Bf=0)
1)Create:
2)Insert:
3)Delete:
4)Print:
5)Quit:
Enter Your Choice: 3
Enter a data: 5
1)Create:
2)Insert:
3)Delete:
4)Print:
5)Quit:
Enter Your Choice: 4
Preorder sequence:
4(Bf=0) 2(Bf=0) 6(Bf=0)
Inorder sequence:
2(Bf=0) 4(Bf=0) 6(Bf=0)
1)Create:
2)Insert:
3)Delete:
4)Print:
5)Quit:
Enter Your Choice: 2
Enter a data: 43
1)Create:
2)Insert:
3)Delete:
4)Print:
5)Quit:
Enter Your Choice: 4
Preorder sequence:
4(Bf=-1) 2(Bf=0) 6(Bf=-1) 43(Bf=0)
Inorder sequence:
2(Bf=0) 4(Bf=-1) 6(Bf=-1) 43(Bf=0)
1)Create:
2)Insert:
3)Delete:
4)Print:
5)Quit:
Enter Your Choice: 5
Result:
Thus, the concept of AVL Tree was implemented successfully.





No comments:
Post a Comment